Tutorial: Stream and Catchment Delineation

7.3. Calculate Channel Network

The next step is to calculate the channel network.

First we're going to create a layer with the Strahler orders for the rivers by selecting the cells with order equal to or higher than the threshold determined in the previous step. Here we'll use order 8 as threshold.

With the PCRaster Tools plugin, we can only use raster layers in map algebra. If we want to calculate a new boolean layer with strahler >= 8 as True (our channels) and < 8 as False, we need to first create an ordinal raster that consists of cells with only value 8. This can then be used in map algebra.

1. In the Processing Toolbox go to PCRaster | Data management | spatial

2. In the Spatial dialogue type 8 for Input nonspatial. Choose Ordinal for Output data type and strahler as the Mask layer. Call the Output raster layer ordinal8.map.

3. Click Run and Close the dialogue after completion.

Now we're going to create a boolean layer with 1  (True) for all strahler cells that are >= 8:

4. In the Processing Toolbox go to PCRaster | Conditional and boolean operators | comparison operators.

5. In the Comparison Operators dialogue choose strahler as Input raster, >= as Comparison operator and ordinal8 as the second Input raster.

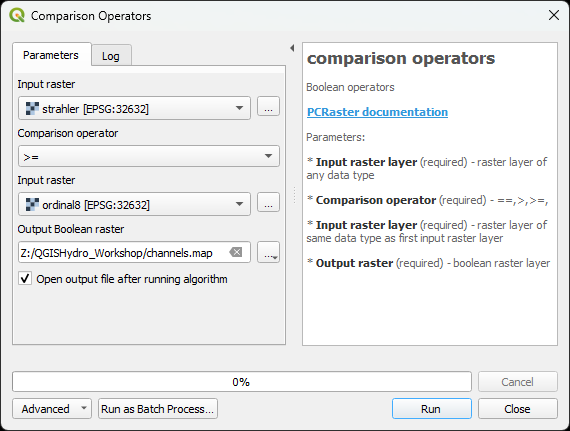
6. Click Run and Close the dialogue after completion.

Now we have a boolean layer with the channels that we can use now to assign the river Strahler orders.

7. In the Processing Toolbox go to PCRaster | Conditional and boolean operators | ifthen.

8. In the If Then dialog, choose channels as the Input Boolean Condition Raster and strahler as the Input True Raster. Call the Output raster channelsstrahler.map.

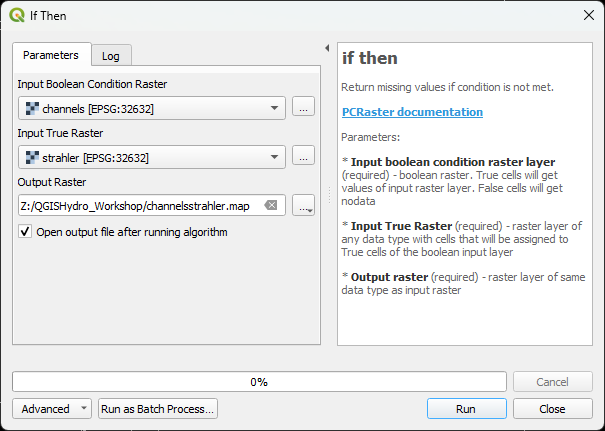
This means: if the channels layer has cells that are True (1), then give those cells the value of the strahler layer. All other cells get "nodata".

9. Click Run and Close the dialog after processing.

Now we have a raster with the Strahler orders for the channels. This can be visualized better as a vector, which will be explained in the next section.